One cannot have too many numbers, really.   Imagine you have a data set that includes many numbers, like U.S. city populations, or the odometer readings for all the cars in an area.  Look at only the first digit of each number in your set of populations or mileage, and count each time 1 through 9 occurred. Each number should occur about the same number of times.  You would have about the same number of 1’s as you would of 2’s or 3’s, right?  The correct answer is somewhat more fun.

The data set has to be scale invariant.  This means that each 1 through 9 digit must have about the same chance of occurring.  Forget it if the data set is the number of legs for everything in the animal kingdom because the occurrences will skew toward even numbers.   Let’s look at monthly account values.  I have a set of these handy.

In the late 1800’s, some mathematician stumbled across the fact that 1 through 9’s will not be equally distributed when looking at certain data sets.   A physicist named Benford lent his name to this property in 1938.  Benford’s Law predicts that 1 will occur about 30% of the time, with 2 occurring about half as many times, and on down the line.  In Figure 1, the first digit distribution is plotted in red for client accounts ending June 2014 (Read what Wikipedia says about Benford’s Law here.)

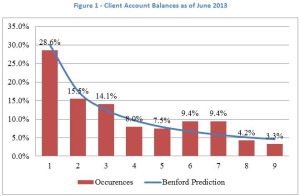
Nice math trick, but what else can we do with Benford’s Law?  Forensic accountants use the law to detect fraud, for example.  How would a notorious company’s quarterly reported net debt (data from Bloomberg) compare to the Benford’s Law predictions I wondered?  In Figure 2, I give a non-rigorous example (from a population of 47) that may or may not have any future predictive value.

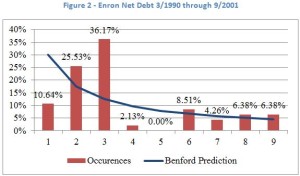
Enron liked to play games with its accounting.  One game was hiding debt from its balance sheet using Special Investment Entities.  Maybe this chart is indicative of Enron’s shenanigans; however, we should not draw conclusions from any one set of data without digging deeper.   There is a lot of research on Benford’s Law that I need to read and I suspect the law may be more useful when looking at companies in aggregate over a time series.  The lesson is that you cannot have too many numbers. Read our More informative blog here